The Big Picture

Its become pretty clear that many people are losing sight of the wood for the trees, or even the twigs, in the latest rounds of the Hockey Stick Wars. Fortunately some of the more intelligent watchers of the debates have realised they need help. So here it is.

What it the Big Picture? From the point of view of climate change, the top level is

The world is getting warmer, we're causing it, and it will continue to get warmer in the future. This is pretty well universally agreed on now.

Going down a level, the point at issue is then the various palaeoclimatic reconstructions of the [[temperature record of the past thousand years]] (or, now, two thousand). Here the important point is ...the increase in temperature in the 20th century is likely to have been the largest of any century during the past 1,000 years... and so on: which you'll doubtless recognise as a quote from the TAR. But more than that, all the headline points that the TAR made about the MBH record it used are true of all the other reconstructions too. So all the nonsense about whether the fall of the Hockey Stick would disprove global warming or whatever is just nonsense. Because there is plenty of backup. The other point that the septics do their best to push is the idea that all the attribution of climate change arises from the palaeo reconstructions. That too is nonsense, & discussed at RC. Or just read the TAR.

Going another level down, we come to the various arguments about the details of the Hockey Stick. Thats the level of the recent RC post Hockey sticks: Round 27, where we discuss two recent GRL papers. This is interesting stuff - if you're keen on statistics. If you're not, and you're baffled by the claims and counter claims, then you have two options: hop back up a level, because you've got to a too specialised for your understanding; or improve your understanding. Don't misunderstand me: there is a lot of interesting work to be done at this level. There are, as shown by the graph, a whole pile of records that agree on the main points but disagree in detail. Resolving this is an active and valuable area of research. If you're interested in policy, though, you've gone too far down. Go back.

Some people think that that the debate over the so-called "hockey stick" temperature reconstruction is a distraction from the development and promulgation of climate policy. And I agree (though I would replace "policy" with "science" cos I'm more interested in the science). And this is what we've been saying in the recent comments at RC. So if anyone were, hypothetically, to enquire why *others* should continue to care about it... Why is this fight important to the rest of us? the answer is: you shouldn't. It isn't. There: that was easy.

Oops: I forgot something and blew my dramatic ending. Sigh. There is (yet another) odd inversion about: the idea that if we were to switch from, say, MBH (less variance) to Moberg (more) that would somehow imply a reduction in expected future warming. That is completely wrong. If the past temperatures varied more, it implies a *higher* sensitivity to forcing, and therefore a *higher* future change.

[Updated to fix broken href; nothing new to see; move along now folks... :-)]

Our pumpkin

Here we see our pumpkin, it being halloween.

I used to rather dislike halloween, but now we're used to it its quite fun. Miranda went out; Daniel stayed in.

Elsewhere: an image of Miranda: in the dark; running; wearing a fairy costume; carrying a toy shopping trolley full of sweets.

In praise of moderation

One of the reasons the various blog fora are valuable is because they moderate comments: which is to say, some are deleted/not posted. The obvious advantage is that this keeps out spam from the porno and online poker folk, rude and abusive nonsense, and the nutters. The obvious disadvantage is that none of the nutters think they are nutters and tend to whine about censorship. This is difficult: no-one is going to spend time and effort writing interesting comments if they think they will be blocked. But my spam/trolling/incivility threshold may be different to yours.

To use an example thats deliberately not the one you're thinking of, over at RC recently one John Dodds has been pushing his own wacky theories of GHE (or lack thereof...); see comments on this thread - 16, 18, etc. RC has probably been too gentle in handling him (nonetheless we (I) got bored in the end). The problem with that stuff is it disrupts the flow of sense.

James Annan suggests posting to sci.environment. If you have no proper newsfeed, go to groups.google.com and its fairly easy. Sci.env has the advantage (?) of being unmoderated, and of course it could aggregate stuff across many blogs, instead of the balkanised blogscape that exists. Why not try it? If your comments here are sufficiently valuable, post them there too, and watch them drown under a sea of junk. An interesting reverse experiment is being tried by mt, who has tried copying a posting from sci.env to his blog to try to have a more sensible debate there, but it doesn't seem to be working.

Refs

* Your comment was denied for questionable content...
* “like being inside Hansens head”
* Moderation at The Conversation - ATTP

Shaken by Tossers. Or not.

Eli Rabbett is laying into Taken by Storm. He has a link to their "briefing" if you really want to read it (I found this via Tim Lambert, who provides you with a link to his earlier demolition).

But what I wanted to discuss was not their arguments, but why they have been totally ignored. And they have been. Not even the knee-jerk septics have done more than nod in their direction.

Firstly, because their idea that global mean temperature is meaningless is such obvious pap that anyone can see that.

Secondly, because their arguments to try to prop up this assertion are sufficiently convoluted that there is not the slightest chance of non-specialists understanding them.

The latter I think is important. If you want to sound off as a GW septic, you need a good sound bite that appears to make sense. Waving your glass at a party saying "of course, global temperature doesn't exist, because..." and then trying to spout pages of gobbledegook that you can't remember is just going to make you sound like a fool.

The obvious contrast is with the M&M attack on the MBH hockey stick stuff. Here, instead of trying to replace the bleedin' obvious with some subtle convolutions, they are trying to attack a fairly subtle technique and pick nits in it. This is far easier to sell, and it has.

Exxonmobil title-tattle: www.europeanvoice.com

EuropeanVoice (which appears to be a business of The Economist) is running a meeting "Climate Change Now: what can Europe deliver?". The blurb sayeth;

With climate change at the top of the G8 and UK Presidency agendas, how can real progress be made in achieving the necessary reductions in CO² [sic] emissions? What can governments and industry do now to deliver cleaner solutions to our energy and transport needs?

The most recent scientific assessments suggest that the climate is changing even faster than previously thought and the pressure is even greater to develop and deliver new technologies which can dramatically reduce greenhouse gases now and in the short- to medium-term.

What more should governments be doing through fiscal or other financial measures to support R&D and innovation and help industry boost the process?

In the run-up to the COP-11 Kyoto talks in Montreal, this conference aims to assess the EU's key objectives going into the talks and policy-makers' and industry's response to the challenges.

Nothing especially weird there (though t' Economist would normally downplay recent scientific assessments suggest that the climate is changing even faster than previously thought and the pressure is even greater to develop and deliver new technologies) until you notice that the sponsor is... Exxonmobil. Exxon used to be heavily anti-GW (this from 2000 is distinctly mendacious, but still I must admit on the cautious side), now its hard to find their views. This from 2003 pushes uncertainty and says nothing really about the state of the science; not much change from 2001. And by 2005 nothing much has changed: they have no position at all on whether the world has warmed and how much it might in the future.

Perhaps they are dipping their toe in the water... to see how warm it is?

Butterflies: notes for a post

[Updated: see end]

This is more in the nature of notes for a proper post, but I'll put it here. If you want to read some sense, check James Annan: still flapping. If you want some nonsense, then follow the link therein to RP :-)

But first: something completely different:



So, I took HadAM3 (64 bit version) and did two runs: one standard, and one where I perturbed the surface pressure at a single grid point (I forget where: somewhere in the Arctic I think) by a tiny amount (1e-10, or was it 1e-12?).

The graph below shows the growth in global-mean area-weighted RMS of the difference of the MSLP field between the two runs:



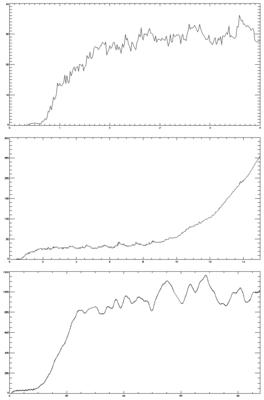
The x-axis is time in days (48 timesteps per day): 0-5 (top); then 0-15 (mid); then 0-89 (bottom). By day about 25, and definitely by day 60, the difference between the runs has saturated: their weather is totally different, so no further growth in RMS occurs. The 5-10 day oscillations in the last month are, I think, what you'd expect to see from weather evolution.

The y-axis is in Pascals. 100 Pascals is an hPa, ie 1 mb. Standard weather charts tend to plot pressure in contours of 4 hPa, so in real weather terms the diffs are sort-of negligible out to about day 15 (although this is a global value, so locally there will probably be bigger values).

There are clearly different phases in the difference growth. After day 25-ish there is a slow rise to saturation. From day about 10 to about 25 there is exponential growth. From day 2 to 10 ish there isn't much growth. And from the start to about day 1 there is another exponential phase.

If you look carefully, you'll see that the diff appears to be zero for the first few timesteps. This isn't really true. But the model output (as opposed to its internal variables) has been converted from 64 to 32 bit floats; and the difference is identically zero at 32 bit (but not 64).

Meanwhile, its interesting to look at the pattern of the diffs.



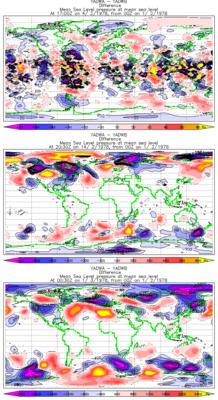
The top pic is about day 4 (in the not-much-happening phase). The middle, day 15 (in the exp growth). The bottom, day 31 (saturated). Note that the pics have a different contour interval. By days 15/31 we're into "real meteorology" and hence the MSLP field is most different in extratropics, as it always is (its tropical dynamics, folks). The fact that the biggest diffs on day 4 are in the tropics (is this convection being jigged?) says we're in a different regime, but I'm a bit unsure.

So there we are for now. Over to you, James.

[The original post was oct 15. I've updated the timestamp.

Update: I've been playing with the timestep-dependence of this. In the pic below, the black line (solid) is run "a" (std) minus run "b" (small pert); black dashed is a-c, where "c" is a different small pert. Blue is the same but for with all three runs done at 1/2 the timestep. Red also, but for 1/4 the timestep. The std timestep is half hour. There are plenty of caveats here: firstly, that this is really only playing. Secondly, that all I did was change the value marked timestep (actually, the value marked "steps per period" from 48 to 96 to 192) without checking that anything was going hideously wrong elsewhere. Thirdly, that if you compare this to the previous plot you'll notice that its spikier: because its 6-h data (instantaneous) not timestep data. Fourthly, that even if nothing is going hideously wrong, changing the timestep does give a different model (is the climatology the same? I don't know. Maybe). For example, the atmos is fourier-filtered at the poles for CFL reasons. A smaller timestep means less area if filtered.

Also: to answer JA's q: does the pert grow one-box-per-timestep (ie, unphysically?). Well no. It grows faster than that, because, ha ha, the perturbation is within the filtering zone so it grows into the entire northern polar cap within a few timesteps.

But: the plot below shows that the initial growth is *slower* with smaller timestep (well even this is complex: the 1/2 timestep run grows faster up to day 1; but then the "plateau" level reached by it is lower between days 2 and 10; and the 1/4 timestep plateau is lower again. Does this mean that a very very small timestep (arguably, as physical reality has?) would have a very low (zero?) plateau? I must try some even shorter timesteps. BUT then you end up in territory where the model was never designed for and it becomes rather dodgy.




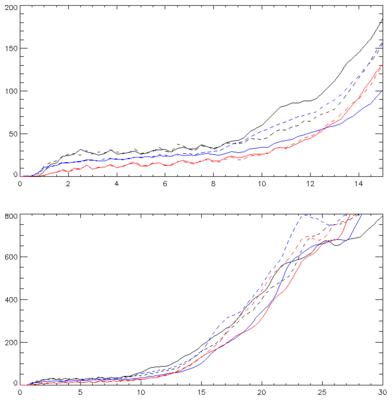
Having 3 different runs at each timestep (more would be nice of course) allows you to see that during the day 15-30 growth phase, the timestep doesn't matter. But earlier, it clearly does.

Curious. I wonder what it means...

ps: sorry James. I'll get back to it :-(

The political post

I do one every now and again. The Steve Bell cartoon in todays Grauniad triggers this one...



I don't know if that will work past tomorrow... If you're wondering about the ?, then maybe you need Deltoid.

Also, I just found (via Dynamics of Cats) this.

WSJ: Yet more Jolly Hockey Sticks, and Barton, et al.

There is a WSJ article "Global-Warming Skeptics Under Fire" (love the title...).

Anyway, the initial point is that it contains some quotes from various parties:

One study, from researchers at the GKSS Research Center in Geesthacht, Germany, confirmed "a glitch" in Dr. Mann's work but "found this glitch to be of very minor significance" when applied to some computer-generated models of climate history, according to a statement released by lead author Hans von Storch.

The other study, by Woods Hole Oceanographic Institution fellow Peter Huybers, argued the Canadians had overstated the effect of the problem. "The truth is somewhere in between, but closer to Dr. Mann," Dr. Huybers said. Both Dr. Huybers and Eduardo Zorita, a collaborator of Dr. von Storch, agreed they had yet to address all of the Canadians' criticisms.

The complex debate, which turns on statistical technicalities, isn't likely to end soon. In replies published in the same issue of the journal, Mr. McIntyre and Mr. McKitrick defended their conclusions. "We are not withdrawing an inch," Mr. McIntyre said in an interview.

The dispute was the subject of a page-one story in this newspaper in February.

Some scientists believe the dispute has more political weight than scientific significance. That's because, they say, other studies of past temperatures also indicate they are higher now, on average, than at any time in past 1,000 years, and perhaps far longer. "A number of studies all come to the same conclusion," Dr. Mann said.

However the WSJ, as is traditional, makes the usual mistakes: The new findings are the latest round in a politically charged dispute over the "hockey stick," a widely publicized graphic showing that temperatures during the late 20th century were likely higher than at any time in the past 1,000 years.. *All* the reconstructions show this, not just the MBH versions.

But also interesting is a statement from Bartons committee:

Mr. Neal said the committee staff hasn't yet begun a detailed analysis of the information it collected from scientists.

Hasn't yet begun? What are these people up to? They demand all this stuff and then do nothing with it? Well, OK, so the answer is obvious: having been slapped down by various people, including and number of scientists and by Boelert (sp?), Barton issued an aggressive statement some while back... and then ran away. However, if anyone has sightings of Barton actually doing anything on the GW/MBH front, do post a comment.

von S on the Hockey Stick

There has been a certain amount of argy-bargy between von Storch and MBH which has lead some people, I think, to mistake von S's position. A recent GRL paper goes some way to clarifying things. Read the RC post on this for refs, and the pdf etc.

As far as I can see, Von S and Zorita basically re-do the stuff from their Science paper, but trying the different centering techniques. And they discover... that it doesn't make much difference. I could have told them that (here though obviously I never quite finished it...). They say:

Our results, derived in the artificial world of an
extended historical climate simulation, indicate therefore
that the AHS does not have a significant impact but leads
only to very minor deviations.

All is, of course, not sweetness and light. There is more to come, I think.

Gems from sci.env

Some gems from sci.environment. First, on the good-old global cooling stuff, someone (mynym) has managed to find some old newspaper cuttings that are relevant, all the way back to 1956! This is interesting, because its far earlier than previously suspected. But, its newspapers not science.

Elsewhen, someone who I will be kind enough not to name said:

> Momentum is not conserved in the same way as mass and energy.

And James "take no prisoners" Annan replied:

You just broke my...

   +--------------------------------------------+
   \         1  2  3  4  5  6  7  8  9         /
    \     0                            10 /   /
     \                                   /   /
      \           CRACKPOT METER        /   /
       \                               /   /
        \                             /   /
         \___________________________/___/
          \                             /
           \.........................../

Your comment was denied for questionable content...

...so I'll post it here. The blog in question is RP Jr, the post this which he entitled "Tag Team Hit Job".

My comment was:

Roger, you complain too much. Curry says you say "Let's not worry about *why* we have climate change" and you don't defend yourself against that, but against something else.

and his software says... "Your comment was denied for questionable content. If you believe a legitimate comment was blocked, you may contact the administrator of this site. This site actively blocks or moderates messages with questionable content. If you feel your message is being blocked unfairly, please contact us. Moderated comments will generally be reviewed within 6 hours."

In fact I will contact him too, but I'm putting it here because (a) it was a good excuse for a post and (b) it illustrates the problems with fragmented conversations in the blogosphere. Mind you, RC also filters for content, but AFAIK doesn't tell you that you comment has been sent for moderation.

Congratulations to Ross Chandler

This one won't mean a lot to most people.

For years, Coton village has had a slowly degrading pavillion barely adequate for cricket, football, etc. Various inconclusive repair/refurbish/rebuild plans were mooted, funders approached: nothing worked due to lack of drive, energy and ambition. A few years ago Ross got elected to the Parish council and has been doing his best to drive the project through, against a degree of conservatism (small C) and a decided lack of ability to take risks, even small ones.

Finally, tonight, he has what he needs: permission to rebuild the thing, demolishing the interior structure, and make a bonfire of the burnable bits. Which I think will make it inevitable that the whole thing will go ahead.

This, and my experience of trying to run an after school club despite the thicket of government regulations, is coming close to converting me to the values of entrepreneurship...

Antarctic sea ice trends

After all the excitement about Arctic sea ice trends its time for that far more interesting region, the Antarctic.

I was going to write this the very next day, but had some odd results which took some time reconciling to reality. So this is using the Comiso (Bootstrap) data. Its also using extent, not area. And its 1979 to 2003, because the Bootstrap data at NSIDC is a bit behind the times (this is a good thing: it means its had extra QC checking for weather clearing and other stuff I don't understand).

So what does it look like? Oh, hold on... before I show you, read this:

The usual caveats apply. I've checked my pic a bit but I did this all in an hour at home tonight after spending some time worrying about Ofsted (and if you don't know what that means, consider yourself lucky), so if anything looks madly wrong to you, you may well be right.

So the pic looks like this:



What you're seeing is decadal trends, by month. In the top pic they are expressed as a percentage of the average for that month; in the bottom, they are expressed as absolute (in millions of square kilometers).

I need to emphasise one important point, which is that the Antarctic ice cover has a very strong seasonal cycle. So the percentage figures can be a bit misleading. The biggest % change is in March (the ice minimum) at about 6%; but the biggest absolute change is about 300,000 km sq in May, with a % change of only 3%. This distinction exists for the Arctic too but is rather less important, because the seasonal cycle there is smaller.

Also, if you are looking at the previous post note that the data there is Team not Bootstrap and is area not extent.

In the Arctic (refer previous post), the main features are:

1. Trends are always negative (ie, losing ice) all year round
   
2. They are largest in late summer and autumn (I would naturally say summer, but september is autumn)
   

In the Antarctic, the main features are:

1. Trends are mostly positive, but near zero and sometimes negative in spring/summer
   
2. They are largest in (southern hemisphere) autumn (mar-apr-may)
   

In absolute terms, the largest (mar-apr-may) trends are about half the Arctic ones (reading off the nsidc press release). As to (statistical) significance... my software thinks that March and May are, but only just (95%).

And spatially they look like... in March and September (scale in fraction per decade):



Mixed.

And what (I hear you say) about the climate interpretation of this? Well (I answer) I didn't interpret the Arctic trends and no-one complained. Perhaps because it was all obvious to everyone. You may want to read the start of this old post too.

The best of the last, the cleanest star they ever had

Or, the Best of Stoat. And in fact not even that, more a Categorised Stoat. Some things get into more than one category.

1. Global warming: A primer on sources for global warming [2005/09/20]
2. Temperature records: ...the increase in temperature in the 20th century is likely to have been the largest of any century during the past 1,000 years... [2005/10/12]
3. Global cooling: Back to the ice ages: Ice, by Fred Hoyle [2005/09/23]
4. Butterfly effect: Butterflies: notes for a post [2005/10] and Repeatability of GCMs [2005/10/04]; Junk science is junk [2005/09/26]
5. Sea ice: Arctic sea ice trends [2005/09/28]
6. Kyoto etc: Paper Tiger [2005/10/08]
7. Septics: Why are we having a hearing that features a fiction writer as our key witness? [2005/09/28]; Junk science is junk [2005/09/26]
8. Wikipedia: Rita Skeeter [2005/09/22]
9. Misc: Pictures at an exhibition [2005/10/11]; My Office [2005/10/08]; Happy birthday to RealClimate [2005/10/03]; Welcome to RC readers [2005/09/28]; Killer sudoku [2005/09/28]; Misc stuff (reading; blogs; etc) [2005/09/27]; John Houghton caught blogging? [2005/09/24]; Technorati [2005/09/21]

[This is something that I wrote mostly for myself, but left in draft. Now (2017) for my own reasons I'd like it published, so will.]

...the increase in temperature in the 20th century is likely to have been the largest of any century during the past 1,000 years...

The IPCC TAR SPM said:

New analyses of proxy data for the Northern Hemisphere indicate that the increase in temperature in the 20th century is likely to have been the largest of any century during the past 1,000 years. It is also likely that, in the Northern Hemisphere, the 1990s was the warmest decade and 1998 the warmest year (Figure 1b).

naturally, this was a red rag to the septics. Its was based, as it says, on Jones et al., 1998, Mann et al., 1998, 1999 and Briffa, 2000. How does this stack up, when compared against more recent reconstructions?

The answer is, extremely well. There is a nice pic on wikipedia (and I've inlined it above) which shows 10 different reconstructions. Looking at this pic we see that

1. the increase in temperature in the 20th century is likely to have been the largest of any century during the past 1,000 years is true for all of them (and for those that go back further, it looks true of the previous 1000 years too)
   
2. It is also likely that, in the Northern Hemisphere, the 1990s was the warmest decade is also true
   
3. and 1998 the warmest year also true (it happens not to have been exceeded since 1998, and most likely not earlier)
   

Another interesting feature of those graphs is that they all pretty much agree on the temperature at the peak of the MWP as being about 0 on a scale that has "now" as about 0.4 (with the caveat of resolution). The major differences are on the depth of the LIA - about 1600, there is little agreement.

Which is why (you just knew I was coming to this didn't you) all the ho-ha over MBH98 is interesting statistically (perhaps) but irrelevant scientifically. It also ought to be irrelevant politically.

To debunk another couple of myths: idiots sometimes assert that the Hockey Stick (ie, MBH98/99) underpins Kyoto. This is nonsense for any number of reasons, but the most obvious is that Kyoto was negotiated in 1997 and you need to believe in reverse causality to think that a 1998 paper underpinned it.

Another one is pointed out by this RC post: The famous conclusion of the IPCC, “The balance of evidence suggests that there is a discernible human influence on global climate”, does not depend on any reconstruction for the past millennium. It depends on a detailed analysis of 20th Century data. In fact, this conclusion is from the 1995 IPCC report, and thus predates the existence of quantitative proxy reconstructions like the “hockey stick”.

Septics focus on MBH98 because they think they have something to say about it. People, naturally, respond. All this tends to give a rather unbalanced view of where the science is. The palaeo reconstructions are important, but only one strand. There is lots and lots of D+A (DAtDA?) that people tend not to discuss much, rather in the same way that few people discuss detailed solutions of GR much: its just too complex for anyone except specialists.

---

Note, BTW, that "likely" is defined thus: In this Summary for Policymakers and in the Technical Summary, the following words have been used where appropriate to indicate judgmental estimates of confidence: virtually certain (greater than 99% chance that a result is true); very likely (90-99% chance); likely (66-90% chance); medium likelihood (33-66% chance); unlikely (10-33% chance); very unlikely (1-10% chance); exceptionally unlikely (less than 1% chance). The reader is referred to individual chapters for more details.

Pictures at an Exhibition

Sometimes I wonder if I focus a bit too much on this climate stuff... Another question is the intrinsic worth of things. And how to judge their relative value. Which in most cases is impossible.

I've been listening a lot to [[Sviatoslav Richter]] playing [[Picures at an Exhibition]] (specifically the recording in Sofia, 1958, if it matters). This is a wonderful recording which I can listen to again and again. The tone and depth of the piano is marvellous; it sounds far better and fuller than an orchestral version we have.

So how to you balance the relative life-worth of simply learning a pile of notes and how to play them in the right order, as against doing science? Who knows.

And now for our daily dose of climate: "I am not sure how clouds get formed. But the clouds know how to do it, and that is the important thing." (Chao mugger via PF).

The picture has no particular relevance to the post, but I felt it needed one of some sort. Its a grey wood in winter, somewhat below Les Deux Alpes, in february 2002.

My office

I know you must be wondering... what does the office of a famous climate modeller look like? Well, I can't tell you that, but I can show you a picture of mine.

Notice whats on the screen. Of course I'm not actually "in work" at this point.

I'm currently fighting a losing battle against getting the place redecorated and pointless modern plastic desks to replace the nice wooden desks (out of shot). There do seem to be limits to my powers.

On the window, you see one of my hobbies: collecting sugar paper wrappers. I hate restaurants which have sugar cubes in a bowl or those sugar shakers. No, I dont take sugar in my coffee. Also just visible behind my keyboard is the rubber chicken which lays an egg. Everyone finds it oh-so-tasteful.

A paper tiger!

The post title is stolen from John Quiggins post. And his post just about says it all: does this new agreement have any substance? Probably not.

So its time for - ta da - prediction time, since predictions made in advace are always more convincing. I predict: that JQ is right: the Asia-Pacific climate pact will turn out to be empty.

There's a wiki page [[Asia-Pacific Partnership for Clean Development and Climate]].

Repeatability of GCMs

Somewhere in the discussion around and after a post of mine on Junkscience is junk I realised that people just don't understand repeatability in GCMs, or indeed much about them at all. This may be in part because they have assumed "telling us precisely which model you used, which initialisation files and what forcing values you supplied (so we can indulge that repeatability thing" (from http://www.junkscience.com/MSU_Temps/Model_Request.htm) made some kind of sense. Sadly now I can't find where the comments were, so I'll try to make it up.

So... although I'm fairly sure much of this is the same for most modern atmosphere-ocean GCMs, I'm actually talking specifically about [[HadCM3]].

There are two sorts of repeatability: you run the model again, and you get *exactly* the same results down to the last bit. This is call bit-reproducibility. Or, you run the model again, and you get *scientifically* the same result (the same climate; probably the same response to forcing within statistical error) but the exact details of the weather differ. Because the climate is chaotic (in the sense that small initial perturbations rapidly amplify) and GCMs reproduce this well, if your model diverges even slightly from bit-reproducibility it will diverge strongly from it, because the details of the individual weather will be totally different. But the climate (statistics of the weather) will be the same.

Which is a good time to point out that GCMs are really weather forecast models run at a lower resolution but for much longer. When you *see* GCM results you normally see global-mean annual-mean data. Don't be confused by this (as some clearly are) into thinking this is what the model directly outputs. It directly outputs temperatures at each gridpoint (96*73 in the case of hadam3 at std res; and in fact at 19 atmos levels too; and of course all the other model variables too) at each timestep (1/2 hour) and this is then meaned up into what you see.

For scientific purposes, bit-reproducibility is not necessary. The weather isn't supposed to be any individual events anyway, so you don't care if you get different weather. But for computational purposes, its rather useful. Firstly, if you're looking for the bug that caused a model crash, its pretty hard to find if the model isn't going to follow the same path when run again. Secondly, the model runs on multiple processors. Bit-reproducibility means it will follow exactly the same path even if the number of processors is different, or if the decomposition is 2*4 instead of 4*2. Also, a good test of the correctness of the MPP decomposition is to run it on different numbers of procs to check you get the same answer.

But bit-reproducibility is only possible on the same processor type, with the same compiler (probably the same version) and the same compiler options, and exactly the same code, and exactly the same input constants, and exactly the same start files, which are themselves enormous. And of course you have to be competent, which lets out Junkscience right from the start. In theory, from the papers and documentation you can write a version of HadCM3 that would be scientifically equivalent. You have no hope of writing one that is bit-equivalent. Its also possible to run the model in non-bit-reproducible mode if you want to (its slightly faster; for example, for bit-r you need to manage the corss-processor calculations in a particular way to get them to come out exactly the same).

And sometimes you don't want bit-reproducibility. The figure that JS are too stupid to see (SPM fig 4) has an ensemble of model runs deliberately started from different initial conditions so that the weather would be different in each, to get a feel for the range of natural variability. If you started a model (assumed to be 100% correct) back at 1860 with 99.9999% accurately known initial conditions you wouldn't expect it to track the individual years accurately (which is why those stupid sci-fi novels about time-travel, where they wander around being careful not to toouch anything, and only get into trouble when they accidentally crush a butterfly, are nonsense. Just being there, standing in the way of the air currents, is enough to totally change the weather and hence all of history). Hence to know if your model is right, you need an ensemble of runs to bracket the natural variability (and you may get unlucky and find that the real world took an unlikely branch).

Happy Birthday to RealClimate

RealClimate just topped 500,000 visits (ha ha watch out Deltoid we're coming to get you...) and has received a Science & Technology Web Awards 2005 award. They don't say if they're in order or not, but in the list we're 9th (out of 25 I think). Chris Mooney makes it too.

Our post on it is here.

Meanwhile, less noticed, Stoat celebrated its 30,000 visit, and even more importantly my google ads racked up my tenth dollar! Only a factor of 10 to go and I'll get my first cheque.